振型圆平衡法采用多点振动联系检测，并利用Nyquist图以转速为参变量在极坐标中绘制某测点振动响应的矢量圆图，称为模态响应圆，如图7-12中所示的细实线圆。

     能较好地在临界转速分离该阶振型，还可以初步确定主要的不平衡在轴系的哪一跨中，在跨中的哪一侧，对选择校正平面有很大帮助。图7-12为一个单跨对称转子的两个轴承振动的Nyquist图。

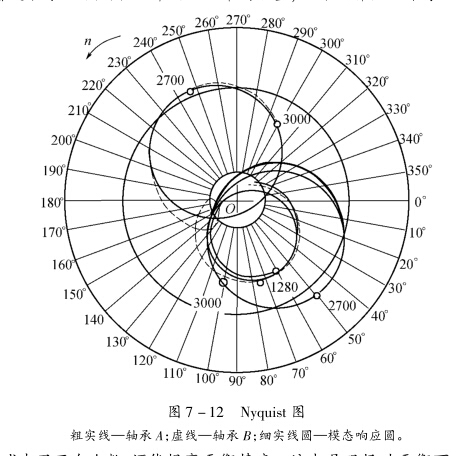
     可以看出，轴承A的振动曲线回执的两个模态响应圆，基本在同一个坐标位置上，即一阶与二阶临界转速的共振直径矢量是基本相同的；而轴承B的振动曲线回执的两个模态响应圆，基本在相反方向坐标位置上，即一阶与二阶临界转速的共振直径矢量是反相的。

     这说明转子不平衡质量主要在轴承A侧，只要在转子靠近轴承A侧的校正平面上加平衡配重，就可以解决一阶与二阶临界转速的振动问题。

     这样不仅减少了开车次数，还能提高平衡精度。这也是现场动平衡可以用一个校正平面解决具有绕性特征的转子不平衡振动的一个原因。至于平衡配重的大小和相位的精确决定需要用影响系数法，这样，振型动平衡法和影响系数法可以结合起来使用。

**电话：400-6616-001

北京时代龙城科技有限责任公司